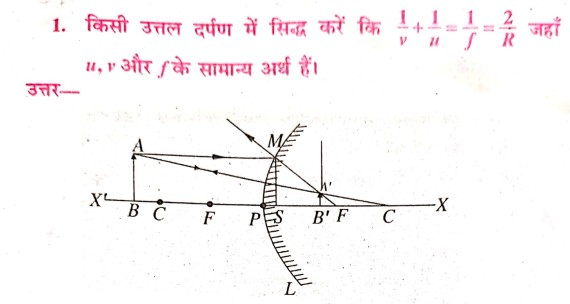
चित्र में L उत्तल दर्पण दिखाया गया है। AB विभ्व XY मुख्य अक्ष पर उदग्र रूप से स्थित है। AB का प्रतिबिंब उत्तल दर्पण में A‘B‘ बनता है जो आभासी है।
BP = विभ्व की दूरी =u
PB’ = प्रतिबिंब की दूरी = v‘
PF = दर्पण का फोकसांतर =ƒ
PC = वक्रता त्रिज्या = R
ΔABC ~ΔA’B’C
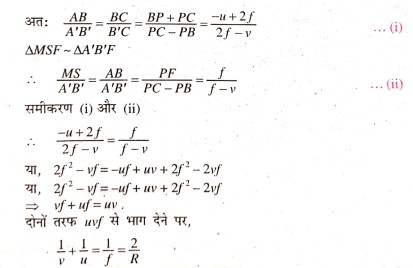
चित्र में MPN एक अवतल दर्पण दिखाया गया है। मुख्य अक्ष XX‘ है। AB एक वस्तु है जो मुख्य अक्ष पर उदग्र खड़ा है। AB प्रकाश किरण मुख्य अक्ष के समांतर है। AM आपतित किरण दर्पण से परावर्तन के बाद फोकस F से होकर गुजरता है। दूसरी किरण दर्पण के वक्रता केन्द्र से होकर जाती है। AN किरण MS किरण को A‘ पर काटती है। AB का वास्तविक उल्टा प्रतिबिंब A‘B‘ बनता है। जो बिंब से छोटा है।
PB = बिंब की दूरी =u
PB = = प्रतिबिंब की दूरी =ν
PF = दर्पण का फोकसांतर = ƒ
और PC = दर्पण की वक्रता त्रिज्या = R
ΔABC ~ΔA’B’C
3. किसी उत्तल दर्पण में सिद्ध करें कि f =R/2 , जहाँ f = फोकसांतर, R = दर्पण की वक्रता त्रिज्या है।
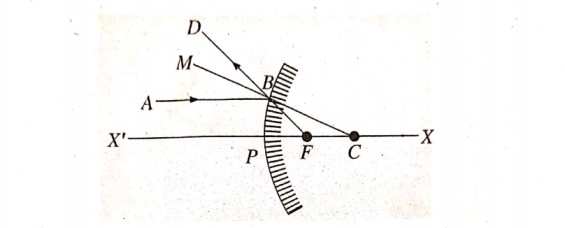
उत्तर⇒ चित्र में एक उत्तल दर्पण को प्रधान अक्ष XX‘ पर रखा गया है। दर्पण का ध्रुव P है। F दर्पण का फोकस और C वक्रता केंद्र है। AB अपवर्तित किरण है। यह दर्पण से परावर्तित होकर BD दिशा में चली जाती है। DB को मिलाने पर यह मुख्य अक्ष के F बिंदु (फोकस) पर मिलाती है। C से B को मिलाया और अपनी दिशा में M तक बढ़ाया गया है।
PF = फोकसांतर =f; PC = वक्रता त्रिज्या = R
अनंत बिंदु से आनेवाली प्रकाश किरण F पर मिलती है
अतः वस्तु का प्रतिबिंब F पर बनता है। यह प्रतिबिंब आभासी है।
∠ABM = i तथा ∠MBD = r
∠i = ∠r परावर्तन के नियम से
∠x = ∠FBC (अंतराभिमुख कोण)
AB || XX’ अतः ∠i = ∠BCF
इसलिए ∠ BCF = ∠FBC
इसलिए BF = FC
अगर B बिंदु P के काफी समीप हैं तो B C = P C
इसलिए BF = PF = FC
PC = PF + FC
R=f +f
इसलिए 2f =R
इसलिए f =R/2
फोकसांतर =1/2 x वक्रता त्रिज्या
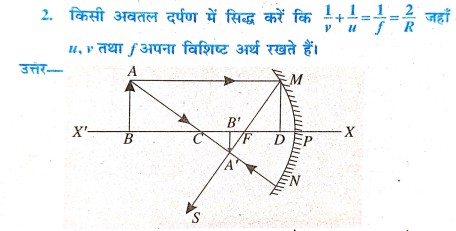
4. अवतल दर्पण में सिद्ध करें कि f=R/2 जहाँ f और R के विशिष्ट मान है।
उत्तर⇒
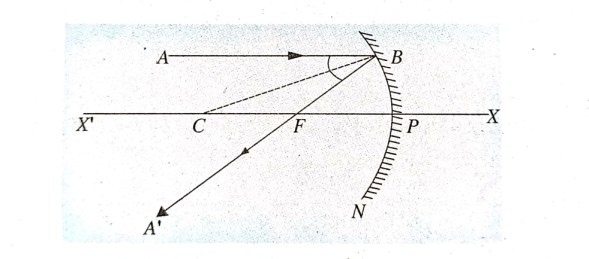
AB प्रकाश किरण मुख्य अक्ष के समांतर है। AB किरण दर्पण से परावर्तन के बाद F (फोकस) से होकर गुजरता है। CB को मिलाया गया है।
∠ABC = ∠CBF = ∠i = ∠r
इसलिए AB \\XX ‘
∠CBF = ∠ABC = ∠BCF
इसलिए ∠i = ∠r
इसलिए अत: CF = BF
अगर B बिन्दु P के काफी समीप है तो BF = PF
इसलिए CP = PF = f (फोकसान्तर) CP = R अवतल दर्पण की वक्रता त्रिज्या है।
इसलिए CP = CF + PF
R= f +f = 2f
इसलिए R = 2f
अतः वक्रता त्रिज्या = 2 x फोकसान्तर
5. पूर्ण आंतरिक परावर्तन को समझावें।
उत्तर⇒ कुछ विशिष्ट परिस्थियों में आपतित प्रकाश को उसकी तीव्रता में बिना किसी विशिष्ट हानि के उसी माध्यम में वापस किया जा सकता है। इस परिघटना को पूर्ण आंतरिक परावर्तन कहते हैं। जब वायु में अपवर्तन कोण का मान 90° होता है तो माध्यम विशेष जिससे प्रकाश किरण चलती है के आपतन कोण को क्रांतिक कोण कहते हैं।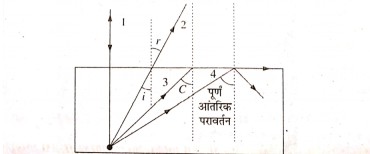 
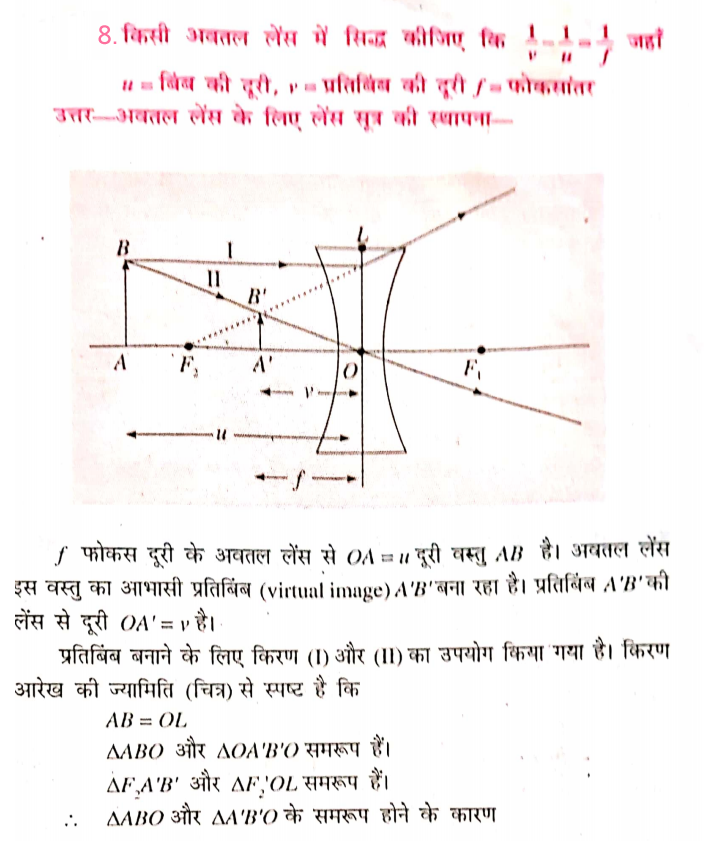
9. किसी उत्तल लेंस के आवर्धन के लिए एक व्यंजक प्राप्त करें।
उत्तर⇒ प्रधान अक्ष के लंबवत प्रतिबिम्ब का अकार h और वस्तु का आकार h का अनपात लेंस द्वारा उत्पन्न आवर्धन कहा जाता है ।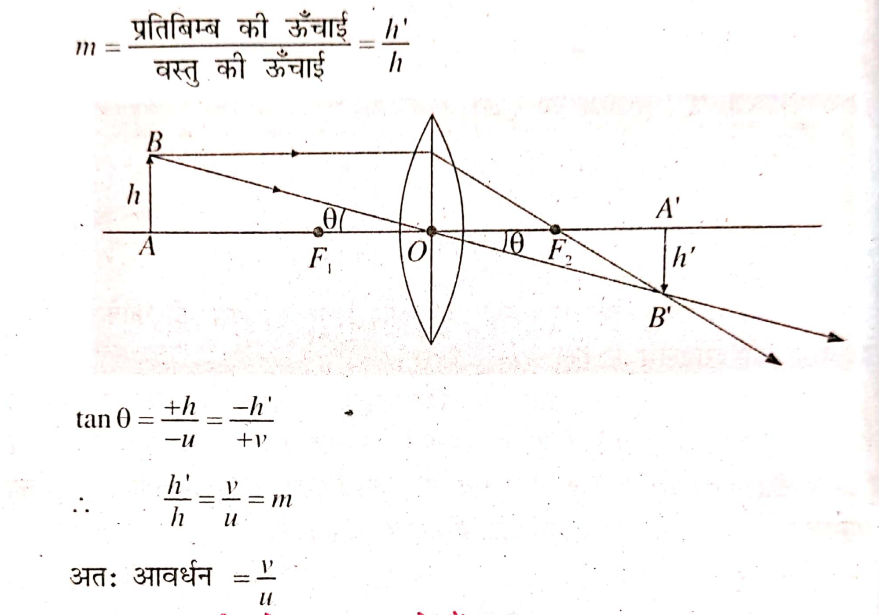
10. आवर्धन से क्या समझते हैं ?
उत्तर⇒ गोलीय दर्पण द्वारा उत्पन्न आवर्धन वह आपेक्षिक विस्तार है जिससे ज्ञात होता है कि कोई प्रतिबिंब बिम्ब की अपेक्षा कितना गुना आवर्धित है। इसे प्रतिबिंब की ऊँचाई के अनुपात के रूप में व्यक्त किया जाता है। यदि ॥ बिम्ब की ऊँचाई हो तथा ‘ प्रतिबिंब की ऊँचाई हो तो गोलीय दर्पण द्वारा उत्पन्न आवर्धन (m) प्राप्त होगा।
इस बात पर ध्यान रखा जाता है कि बिम्ब की ऊँचाई धनात्मक ली जाती है क्योंकि बिम्ब को मुख्य फोकस अक्ष के ऊपर रखा जाता है । आभासी प्रतिबिंबों के लिए प्रतिबिंब की ऊँचाई भी धनात्मक होती है जबकि वास्तविक प्रतिबिंबों के लिए प्रतिबिंब ऊँचाई ऋणात्मक चिह्न से ज्ञात किया जाता है । आवर्धन के मान में ऋणात्मक चिह्न से ज्ञात होता है कि प्रतिबिंब वास्तविक है और आवर्धन के मान में धनात्मक चिह्न बताता है कि प्रतिबिंब आभासी है।
11. अपवर्तनांक से क्या समझते हैं ?
उत्तर⇒ अपवर्तनांक को एक महत्त्वपूर्ण भौतिक राशि, विभिन्न माध्यमों में प्रकाश के संचरण की आपेक्षिक चाल से सम्बद्ध किया जा सकता है। विभिन्न माध्यमों में प्रकाश की चाल भिन्न–भिन्न होती है। हल्के (विरल) माध्यम में प्रकाश की चाल सघन माध्यम की अपेक्षा अधिक होती है। अगर माध्यम 1 से माध्यम 2 में प्रकाश किरणें प्रवेश कर रही हैं तो मान लिया कि माध्यम 1 में प्रकाश की चाल , तथा माध्यम 2 में प्रकाश की चाल V, है। माध्यम 2 का माध्यम 1 के सापेक्ष अपवर्तनांक, माध्यम 1 में प्रकाश की चाल तथा माध्यम 2 में प्रकाश की चाल के अनुपात द्वारा व्यक्त करते हैं।
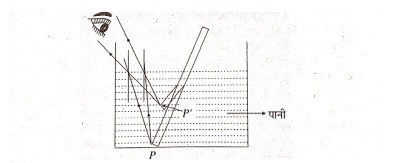
12. किरण-आरेख से दिखावें कि पानी की गहराई किसी बाल्टी में वास्तविक गहराई से कम है।
उत्तर⇒ बाल्टी में पानी लिया जाता है। पेंदे के किसी बिंदु P से निकलने वाले किरण PB और PC क्रमशः वायु में निकलने पर अभिलंब से दूर विचलित हो जाता है।
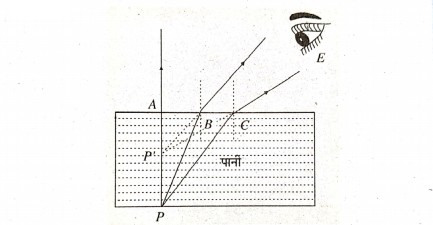
दर्शक प्रकाश की किरणों को P‘ से निकलते हुए देखता है और बाल्टी का पेंदा उठा मालम पड़ता है। यह घटना अपवर्तन के कारण होता है। अतः पानी से भरी बाल्टी की मल–गहराई कम प्रतीत होती है, जिसे बाल्टी को आभासी गहराई के रूप में देख पाते हैं।
13. पानी में रखा सिक्का उठा हुआ मालूम पड़ता है। क्यों ?
उत्तर⇒ पानी के अन्दर रखा हुआ सिक्का कुछ ऊपर उठा हुआ मालूम पड़ता है। यह परिघटना प्रकाश के अपवर्तन के कारण होता है।
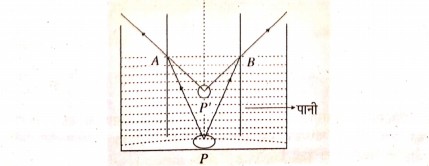
पानी के अंदर बरतन में सिवका की स्थिति P पर है। PA और PB दो आपतित किरणें निकलती हैं। A और B से ये किरणें ज्योंहि वाय माध्यम में अपवर्तित होती है वे अभिलंब से दूर हट जाती हैं। क्योंकि पानी, वायु की अपेक्षा सधन माध्यम है। ये दोनों झुकी किरणें आँख पर P बिंद का आभासी प्रतिबिंब p‘ पर देखता है। ऐसा प्रतीत होता है कि पानी में सिक्का की वास्तविक स्थिति p‘ पर है लेकिन p‘ पर सिक्का का आभासी स्थिति है जो P से ऊपर है। अतः पानी में रखा गया सिक्का देखने पर कुछ उठा हुआ मालूम पड़ता है।
14. पानी के अंदर आधी डूबी हुई पेन्सिल या काँच की छड़ टेढ़ी । मालूम पड़ती है। स्वच्छ चित्र द्वारा समझावें।
उत्तर⇒ पानी में अंशतः डूबी हई पेन्सिल अथवा काँच की छड़ टेढ़ी प्रतात हाता है। यह परिघटना प्रकाश किरणों के अपवर्तन के कारण होता है। प्रकाश की किरण सघन माध्यम से विरल माध्यम की ओर चलती हैं और यह अभिलंब से दूर हट जाती है। दर्शक P बिंदु की स्थिति P‘ पर देखना है। अत: पेन्सिल के नीचे का छोर थोड़ा ऊपर उठा हुआ तथा पेंसिल अपवर्तक सतह पर थोड़ा टेढ़ा दीखता है। 